Brian Beckman
physicist and member of
No Bucks Racing Club
P.O. Box 662
Burbank, CA 91503
©Copyright 1991
Most autocrossers and race drivers learn early in their careers the importance of balancing a car. Learning to do it consistently and automatically is one essential part of becoming a truly good driver. While the skills for balancing a car are commonly taught in drivers' schools, the rationale behind them is not usually adequately explained. That rationale comes from simple physics. Understanding the physics of driving not only helps one be a better driver, but increases one's enjoyment of driving as well. If you know the deep reasons why you ought to do certain things you will remember the things better and move faster toward complete internalization of the skills.
Balancing a car is controlling weight transfer using throttle, brakes, and steering. This article explains the physics of weight transfer. You will often hear instructors and drivers say that applying the brakes shifts weight to the front of a car and can induce oversteer. Likewise, accelerating shifts weight to the rear, inducing understeer, and cornering shifts weight to the opposite side, unloading the inside tires. But why does weight shift during these maneuvers? How can weight shift when everything is in the car bolted in and strapped down? Briefly, the reason is that inertia acts through the center of gravity (CG) of the car, which is above the ground, but adhesive forces act at ground level through the tire contact patches. The effects of weight transfer are proportional to the height of the CG off the ground. A flatter car, one with a lower CG, handles better and quicker because weight transfer is not so drastic as it is in a high car.
The rest of this article explains how inertia and adhesive forces give rise to weight transfer through Newton's laws. The article begins with the elements and works up to some simple equations that you can use to calculate weight transfer in any car knowing only the wheelbase, the height of the CG, the static weight distribution, and the track, or distance between the tires across the car. These numbers are reported in shop manuals and most journalistic reviews of cars.
Most people remember Newton's laws from school physics. These are fundamental laws that apply to all large things in the universe, such as cars. In the context of our racing application, they are:
The first law: a car in straight-line motion at a constant speed will keep such motion until acted on by an external force. The only reason a car in neutral will not coast forever is that friction, an external force, gradually slows the car down. Friction comes from the tires on the ground and the air flowing over the car. The tendency of a car to keep moving the way it is moving is the inertia of the car, and this tendency is concentrated at the CG point.
The second law: When a force is applied to a car, the change in motion is
proportional to the force divided by the mass of the car. This law is expressed by the
famous equation 
, where 
is a force, 
is the mass of the car, and 
is the acceleration, or change in motion, of the car. A
larger force causes quicker changes in motion, and a heavier car reacts more slowly to
forces. Newton's second law explains why quick cars are powerful and lightweight. The more
and the less you have, the more you can get.
The third law: Every force on a car by another object, such as the ground, is matched by an equal and opposite force on the object by the car. When you apply the brakes, you cause the tires to push forward against the ground, and the ground pushes back. As long as the tires stay on the car, the ground pushing on them slows the car down.
Let us continue analyzing braking. Weight transfer during accelerating and cornering are mere variations on the theme. We won't consider subtleties such as suspension and tire deflection yet. These effects are very important, but secondary. The figure shows a car and the forces on it during a ``one g'' braking maneuver. One g means that the total braking force equals the weight of the car, say, in pounds.
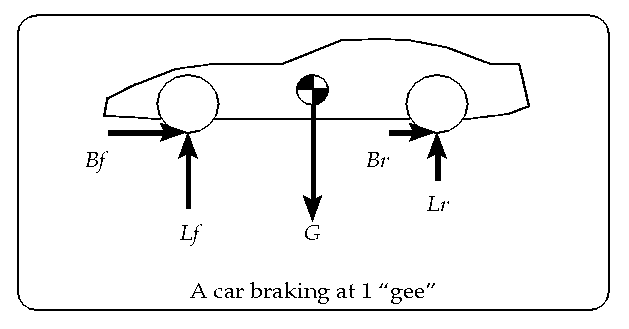
In this figure, the black and white ``pie plate'' in the center is the CG. 
is the force of gravity that pulls
the car toward the center of the Earth. This is the weight of the car; weight is just
another word for the force of gravity. It is a fact of Nature, only fully explained by
Albert Einstein, that gravitational forces act through the CG of an object, just like
inertia. This fact can be explained at deeper levels, but such an explanation would take
us too far off the subject of weight transfer.
is the lift force exerted by
the ground on the front tire, and 
is the lift force on the rear tire. These lift forces are as real as the ones that keep an
airplane in the air, and they keep the car from falling through the ground to the center
of the Earth.
We don't often notice the forces that the ground exerts on objects because they are so ordinary, but they are at the essence of car dynamics. The reason is that the magnitude of these forces determine the ability of a tire to stick, and imbalances between the front and rear lift forces account for understeer and oversteer. The figure only shows forces on the car, not forces on the ground and the CG of the Earth. Newton's third law requires that these equal and opposite forces exist, but we are only concerned about how the ground and the Earth's gravity affect the car.
If the car were standing still or coasting, and its weight distribution were 50-50,
then would be the same as . It is always the case that plus equals , the weight of the car. Why? Because of Newton's first
law. The car is not changing its motion in the vertical direction, at least as long as it
doesn't get airborne, so the total sum of all forces in the vertical direction must be
zero. points down and
counteracts the sum of and , which point up.
Braking causes to be greater
than . Literally, the ``rear end
gets light,'' as one often hears racers say. Consider the front and rear braking forces, 
and 
, in the diagram. They push backwards on the tires, which
push on the wheels, which push on the suspension parts, which push on the rest of the car,
slowing it down. But these forces are acting at ground level, not at the level of the CG.
The braking forces are indirectly slowing down the car by pushing at ground level, while
the inertia of the car is `trying' to keep it moving forward as a unit at the CG level.
The braking forces create a rotating tendency, or torque, about the CG. Imagine pulling a table cloth out from under some glasses and candelabra. These objects would have a tendency to tip or rotate over, and the tendency is greater for taller objects and is greater the harder you pull on the cloth. The rotational tendency of a car under braking is due to identical physics.
The braking torque acts in such a way as to put the car up on its nose. Since the car
does not actually go up on its nose (we hope), some other forces must be counteracting
that tendency, by Newton's first law. cannot be doing it since it passes right through the
cetner of gravity. The only forces that can counteract that tendency are the lift forces,
and the only way they can do so is for to become greater than . Literally, the ground pushes up harder on the front
tires during braking to try to keep the car from tipping forward.
By how much does exceed ? The braking torque is proportional to
the sum of the braking forces and to the height of the CG. Let's say that height is 20
inches. The counterbalancing torque resisting the braking torque is proportional to and half the wheelbase (in a car with
50-50 weight distribution), minus
times half the wheelbase since is
helping the braking forces upend the car. has a lot of work to do: it must resist the torques of
both the braking forces and the lift on the rear tires. Let's say the wheelbase is 100
inches. Since we are braking at one g, the braking forces equal , say, 3200 pounds. All this is summarized in the
following equations:
With the help of a little algebra, we can find out that
Thus, by braking at one g in our example car, we add 640 pounds of load to the front tires and take 640 pounds off the rears! This is very pronounced weight transfer.
By doing a similar analysis for a more general car with CG height of 
, wheelbase 
, weight , static weight distribution 
expressed as a fraction of weight in the front, and
braking with force 
, we can show
that
These equations can be used to calculate weight transfer during acceleration by
treating acceleration force as negative braking force. If you have acceleration figures in
gees, say from a G-analyst or other device, just multiply them by the weight of
the car to get acceleration forces (Newton's second law!). Weight transfer during
cornering can be analyzed in a similar way, where the track of the car replaces the
wheelbase and is always
50%(unless you account for the weight of the driver). Those of you with science or
engineering backgrounds may enjoy deriving these equations for yourselves. The equations
for a car doing a combination of braking and cornering, as in a trail braking maneuver,
are much more complicated and require some mathematical tricks to derive.
Now you know why weight transfer happens. The next topic that comes to mind is the physics of tire adhesion, which explains how weight transfer can lead to understeer and oversteer conditions.